Build a Calendar in InDesign
Everyone needs a calendar sooner or later. Learn how to easily build one inside InDesign using a script we've provided for you.
by: David Blatner
I'm always amazed at how many people need to make calendars: big calendars, small calendars, one-month calendars, full-year calendars. Fortunately, InDesign offers a "make me a calendar" feature... no, sorry, not really. But it's so easy to make a calendar in InDesign that it's as though the program did have such a feature. The trick is to download a template or script that does a lot of the work for you.
Use a Template
One of the best and easiest ways to make a calendar is to use a template designed by someone else. Search for the word "calendar" in the InDesign section at the Adobe exchange and you'll find a number of free templates.
While most are year-specific, there are a couple called "25-year calendars," such as the clever one rusty Wright built. these contain 28 different master pages, each of which reflect one possible month layout. For example, if January 1 begins on a Monday, you'd apply that particular master page layout to your January document page.
You can also find calendar templates for a small fee. Chuck Green's The InDesign Ideabook includes several calendars on its accompanying disc. note that most of these templates have paragraph styles for each calendar element, so changing the typefaces and overall look and feel of the calendar is typically as simple as editing a few styles.
Use a Script
If you need more flexibility than a template offers, consider using a script to build your calendar for you. One of the most popular and easiest scripts available is called Calendar Wizard, written by Scott Selberg (based on ideas and code written by Jan Suhr, Robert Cornelius, and Steve Nichols). Here's how it works.
1 - Download, install, and run
Calendar Wizard 0.9 is available on the adobe
exchange, but we've made it easy for you by commissioning a special, newer version of the script. to download the Calendar Wizard 2.0 file, go to
http://downloads.indesignmag.com/supportfiles/. Once you download and decompress the folder, it's a tiny 13 KB file and written in JavaScript, so it works on both Mac OS and Windows.
After you download and unzip it, install it by putting it inside the InDesign > Presets > Scripts folder (in CS2) or inside the InDesign > Scripts > Scripts Panel folder (in CS3).
Note that this gives you four files: the script to make the calendar, a script to realign the calendars, a script to fit a calendar to a frame, and a readMe file with lots of good information on how the script works and how to use it.
After installation, you'll immediately find it in
InDesign's Scripts panel (Window > Automation
> Scripts). To run it, double-click on it in the panel
(Figure 1). If you get an error at this point, simply open
a document, then double-click on the script again.
2 - Choose the Date Range
The first two items in the Calendar Wizard dialog
box (Figure 2) are straightforward: They let you
choose the starting and ending months and year(s)
for your calendar. You can pick any year from 2004 to
2017. If you were hoping for 2018, you'll have to wait
until next year; the script looks only 10 years ahead.
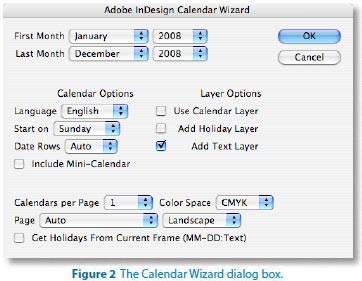
3 - Pick the Calendar Options
You can choose English, German, French, or
Spanish from the Language pop-up menu to
change the way the text appears (Figure 3). Next, pick
whether you want the left column to be a Sunday or a
Monday.
Note that some months take up only five rows and
some take six. (If February 1 lands on a Sunday, it'll
take 4 rows.) In general, you should choose Auto from
the Date Rows pop-up menu, but if you want to force
all the months to the same number of rows, you can
choose that here.
If you turn on the Include Mini-Calendar checkbox,
you'll get small versions of the previous and next
month's calendars inset into each month's calendar.
This takes longer to build and creates many more
objects on your page, but it can be a good addition to
one-month-per-page wall calendars.
Adding Holidays to Your Calendar
While version .9 of Calendar Wizard is on the Adobe
Exchange, the script's author, Scott Selberg, has
provided us with the newest version of Calendar
Wizard at http://downloads.indesignmag.com/
supportfiles/. Version 2.0 has several new features,
including creating and applying table styles and the
ability to insert the names of holidays into the proper
date locations automatically.
The trick to adding holiday names to your calendar
is to type them using a special format into an
InDesign text frame. Each holiday should be on its
own line, and in this format:
1-1:New Year's Day
2-14:Valentine's Day
Don't put a zero at the beginning of each month!
Just the month, hyphen, then date.
You can find lists of holidays on the Web at
timeandate.com and on Wikipedia.
4 - Choose Layer Options
One of the coolest things about CalendarWizard
is that it can make good use of the Layers panel.
If you turn off all the checkboxes in the Layer Options
section, the whole calendar is placed on Layer 1.
However, I prefer to turn on all three checkboxes to
produce the following:
- The calendar grid (along with numbers and text) on a
layer called "calendar"
- An empty duplicate of the grid on a layer called
"calText," which lets you easily add text at the top of
each calendar cell.
- An empty duplicate of the grid on a layer called
"calHolidays," which lets you easily add the names
of holidays at the bottom of each cell. If you add
holidays automatically (see the sidebar "Adding
Holidays to Your Calendar"), this layer is always
created for you.
5 - Pick a Page Setup
The last settings in the dialog box control how
calendars are laid out on the page. You can pick
how many months should fit on each page, whether
the page layout should be portrait or landscape, and
whether to create a new document or fit the calendar
into the current document (Figure 4).
If you had a text frame selected on your page
when you launched the script, you can also choose
Current Text Frame from the Page pop-up menu. In
that case, the script places the calendar (but only a
single month) into that frame. That's particularly handy
when you need a calendar to fit a specific size and
position on your page. When the pop-up menu is set
to Auto, and you have a text frame selected, the script
automatically places the calendar into that frame.
6 - Create the Calendar
When you click OK, the script jumps into action
and builds the calendar (Figure 5). This can
take up to a minute or more (especially with minicalendars),
so be patient.
Unless you've targeted a text frame for a singlemonth
calendar or you have a text frame selected
in your current document, the script builds a new
document for you. The size and margins of that
document are based on the last-used document
preset (that is, whatever you last chose in the Document
Preset pop-up menu in the New Document
dialog box).
7 - Add Custom Text
This script creates calendars as tables
inside text frames. The numbers and
text are in the cells of one table, and—if
you added a calHoliday layer or a calText
layer—you'll find one or more duplicate
tables on other layers. If you want to insert
additional holidays into the calendar, open
the Layers panel and Option/Alt-click on
the lock column next to calHolidays layer
(Figure 6). This locks all the other layers, and
leaves this layer unlocked. Now you can click
with the Type tool inside a table cell and
type the holiday. Similarly, to add to the Text
layer, Option/Alt-click next to the calText
layer to lock all the other layers.
8 - Format the Calendar
The calendars that CalendarWizard creates aren't
exactly beautiful right out of the box. Fortunately,
the script builds a number of paragraph styles, table
styles (CS3 only), and color swatches. Edit the styles
and your calendars update to look far better.
If you're going to print your calendar, check the
color space of the three color swatches it creates:
DayCellBackground, DayTextColor, and Holiday. In the
publicly available version .9, they're all specced as RGB
colors. If you use the script attached to this PDF, they're
likely in CMYK mode. But if they're RGB, then right-click
(or Control-click with a one-button mouse on a Mac)
on each of these colors in the Swatches panel, choose
Swatch Options, and set the Color Mode to CMYK. The
two DayCell swatches control the color of the text and
the cells behind the day names ("Monday," "Tuesday,"
and so on). The Holiday swatch controls the color of
any holidays you type on the calHoliday layer.
The first paragraph style you should change is the
"cal_base" style, on which all the other styles are based.
By default, the font is set to 12-point Times. Change
this font, and it will change throughout the calendar.
If you're using Calendar Wizard 2.0 in InDesign CS3,
you can also edit the styles in the Cell Styles and Table
Styles panels (Figure 7). For example, if you
want the cell containing the month name to have a
particular fill color, change the cal_header cell style.
To change the border around the frames, change the
table style called "calendar."
Laying out a Document Vertically
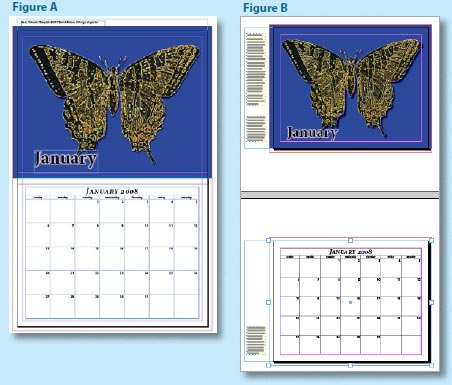
InDesign is so flexible, you'd think it would be easy to lay
out a spread vertically instead of horizontally—so that the
spine is at the top and bottom, which many wall calendars
require. Unfortunately, it isn't easy. However, Anne-Marie
Concepción came up with a great workaround you can read
in full at InDesignSecrets.com. Here's the gist:
- Lay out the entire spread on a single page. For a
12-month calendar, you'd create 12 tall pages, each
containing the image and calendar (Figure A).
- Save the InDesign document.
- Create a new InDesign document at the finished page
size (half the height of the calendar).
- Place the original InDesign document into the new one.
(If you're using CS2 or earlier, you'll need to export a PDF
of the tall document first and import that instead.) The
first page of the new document should contain the top
half of the tall document; the second page contains the
lower half; and so on. If you used bleed guides in the
original, full-height document, you'll need to adjust for
that in the Import Options dialog box when you import
it.
In this model, you design in the tall document and
print from the half-height one (Figure B). Then,
whenever you edit the tall document, update the modified
links in the Links panel of the print version.
By the way, if you're making more than one
calendar, just set the styles in one document and then
choose Load Paragraph Styles in the Paragraph Styles
panel menu to copy them from one file to another.
9 - Resize or Realign the Calendars
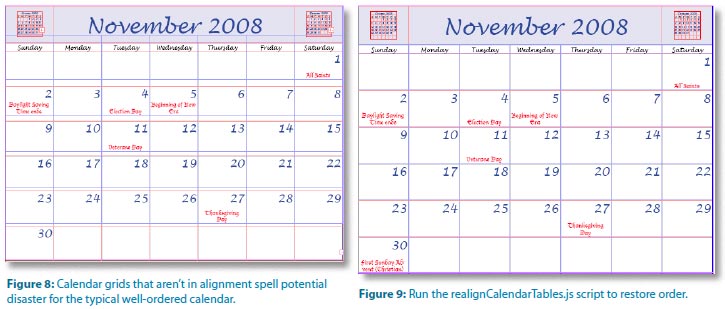
When you've created holiday and text layers, it
can be frustrating if one of the grids gets out of
alignment (Figure 8). Let's say you change the height
of the month name to be too large for its row. You can
use the Type tool to adjust the row height, but now the
holiday and text tables are out of alignment. Simply
turn to a second script called realignCalendarTables.js,
which comes with CalendarWizard.
Double-click the realignCalendarTables.js script
to launch it. If you have one of the tables selected, it
assumes that the selected table is the master—the one
all other tables should match. If no calendar frames are
selected, the script asks which calendars you want to
realign (I usually choose All) and which layer should it
assume is the master calendar. This script is easy and
painless and saves a huge amount of time (Figure 9).
If your frame size changes, you'll want to use the
fitCalendarToFrame.jsx script, which does pretty much
exactly what it says: The calendar stretches out to
match the new frame size. Note that if you've adjusted
rows or columns, those changes are lost—all the cells
are of equal size after you use this script.
Figure 7: CS3's Cell Styles and Table Styles panels.
All trademarks are the sole property of their respective owner.
